Code: Alles auswählen
Manipulate[
c = 1; v = c/2; γ = Sqrt[1 - v^2];
t1 = γ/(c + v);
t2 = 1/Sqrt[c^2 - v^2];
t3 = γ/v;
t3a = t3 + 1/2/Sqrt[c^2 - v^2];
t4 = 8/3 γ;
La = Line[{{0, 0}, {0, 1}, {1 γ, 1}, {1 γ, 0}, {0, 0}}];
Ld = Line[{{0, 1 - γ}, {0, 1}, {1, 1}, {1, 1 - γ}, {0, 1 - γ}}];
Le = Line[{{0, 0}, {0, 1}, {1, 1}, {1, 0}, {0, 0}}];
Lf = Line[{{0, 0}, {0, 1}, {1, 1}, {1, 0}, {0, 0}}];
Lg = Line[{{0, 0}, {0, 1}, {1, 1}, {1, 0}, {0, 0}}];
Lh = Line[{{0, 0}, {0, 1}, {1, 1}, {1, 0}, {0, 0}}];
Li = Line[{{0, 0}, {0, 1}, {1, 1}, {1, 0}, {0, 0}}];
P1a = {PointSize[Large], Black, Point[{1 γ - v t, 1}]};
T1a = Text[StyleForm["v", FontSize -> 9],
{1 γ - v t, 1 + 0.04}];
P2a = {PointSize[Large], Red, Point[{1 γ - (c + v) t, 1}]};
T2a = Text[StyleForm["c+v", FontSize -> 9],
{1 γ - (c + v) t, 1 + 0.04}];
P3a = {PointSize[Large], Blue,
Point[{1 γ, 1 - Sqrt[c^2 - v^2] t}]};
T3a = Text[
StyleForm[
"\!\(\*SqrtBox[\(\*SuperscriptBox[\(c\), \(2\)] - \
\*SuperscriptBox[\(v\), \(2\)]\)]\)", FontSize -> 9],
{1 γ + 0.1, 1 - Sqrt[c^2 - v^2] t}];
P1b = {PointSize[Large], Black, Point[{1 γ - v t, 1}]};
T1b = Text[StyleForm["v", FontSize -> 9],
{1 γ - v t, 1 + 0.04}];
P2b = {PointSize[Large], Red,
Point[{0, 1 - Sqrt[c^2 - v^2] (t - t1)}]};
T2b = Text[
StyleForm[
"\!\(\*SqrtBox[\(\*SuperscriptBox[\(c\), \(2\)] - \
\*SuperscriptBox[\(v\), \(2\)]\)]\)", FontSize -> 9],
{0 - 0.1, 1 - Sqrt[c^2 - v^2] (t - t1)}];
P3b = {PointSize[Large], Blue,
Point[{1 γ, 1 - Sqrt[c^2 - v^2] t}]};
T3b = Text[
StyleForm[
"\!\(\*SqrtBox[\(\*SuperscriptBox[\(c\), \(2\)] - \
\*SuperscriptBox[\(v\), \(2\)]\)]\)", FontSize -> 9],
{1 γ + 0.1, 1 - Sqrt[c^2 - v^2] t}];
P1c = {PointSize[Large], Black, Point[{1 γ - v t, 1}]};
T1c = Text[StyleForm["v", FontSize -> 9],
{1 γ - v t, 1 + 0.04}];
P2c = {PointSize[Large], Red,
Point[{0, 1 - Sqrt[c^2 - v^2] (t - t1)}]};
T2c = Text[
StyleForm[
"\!\(\*SqrtBox[\(\*SuperscriptBox[\(c\), \(2\)] - \
\*SuperscriptBox[\(v\), \(2\)]\)]\)", FontSize -> 9],
{0 - 0.1, 1 - Sqrt[c^2 - v^2] (t - t1)}];
P3c = {PointSize[Large], Blue,
Point[{1 γ - (c + v) (t - t2), 1 - Sqrt[c^2 - v^2] t2}]};
T3c = Text[StyleForm["c+v", FontSize -> 9],
{1 γ - (c + v) (t - t2), 1 - Sqrt[c^2 - v^2] t2 - 0.04}];
P1d = {PointSize[Large], Black, Point[{0, 1 - v (t - t3)}]};
T1d = Text[StyleForm["v", FontSize -> 9],
{0 - 0.03, 1 - v (t - t3)}];
P2d = {PointSize[Large], Red,
Point[{1/2 + Sqrt[c^2 - v^2] (t - t3), 1 - γ}]};
T2d = Text[
StyleForm[
"\!\(\*SqrtBox[\(\*SuperscriptBox[\(c\), \(2\)] - \
\*SuperscriptBox[\(v\), \(2\)]\)]\)", FontSize -> 9],
{1/2 + Sqrt[c^2 - v^2] (t - t3), 1 - γ - 0.08}];
P3d = {PointSize[Large], Blue,
Point[{0, 1 - 1/Sqrt[3] + (c - v) (t - t3)}]};
T3d = Text[StyleForm["c-v", FontSize -> 9],
{0 - 0.049, 1 - 1/Sqrt[3] + (c - v) (t - t3)}];
P1e = {PointSize[Large], Black, Point[{0, 1 - v (t - t3)}]};
T1e = Text[StyleForm["v", FontSize -> 9],
{0 - 0.03, 1 - v (t - t3)}];
P2e = {PointSize[Large], Red,
Point[{1, 1 - γ + (c - v) (t - t3a)}]};
P3e = {PointSize[Large], Blue,
Point[{0, 1 - 1/Sqrt[3] + (c - v) (t - t3)}]};
T3e = Text[StyleForm["c-v", FontSize -> 9],
{0 - 0.049, 1 - 1/Sqrt[3] + (c - v) (t - t3)}];
Graphics[
Piecewise[{
{{La, P1a, P2a, P3a, T1a, T2a, T3a}, t <= t1},
{{La, P1b, P2b, P3b, T1b, T2b, T3b}, t > t1 && t <= t2},
{{La, P1c, P2c, P3c, T1c, T2c, T3c}, t > t2 && t <= t3},
{{Ld, P1d, P2d, P3d, T1d, T2d, T3d}, t > t3 && t <= t3a},
{{Ld, P1e, P2e, P3e, T1e, T3e}, t > t3a && t <= t4}
}], PlotRange -> {{-0.25, 1.25}, {-0.1, 1.1}},
Frame -> True],
{t, 0, t4}]
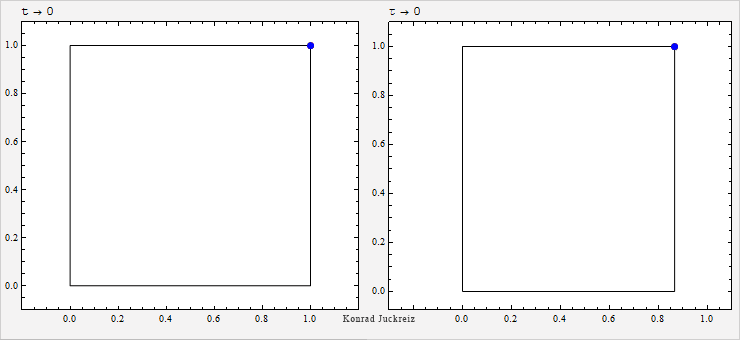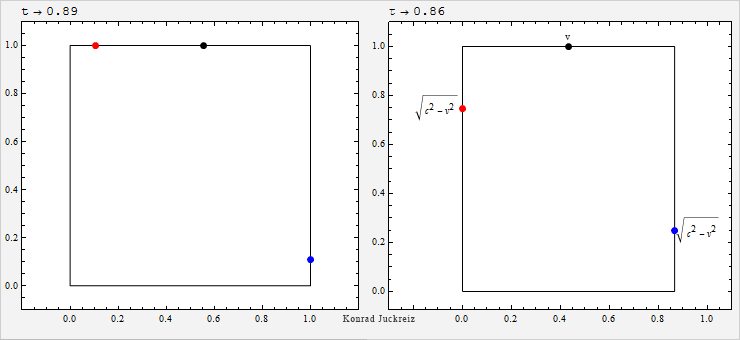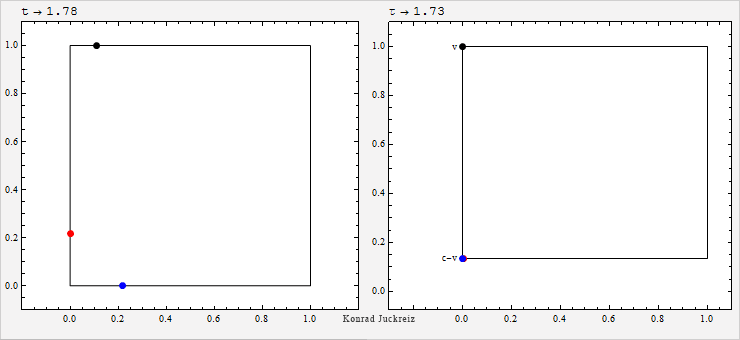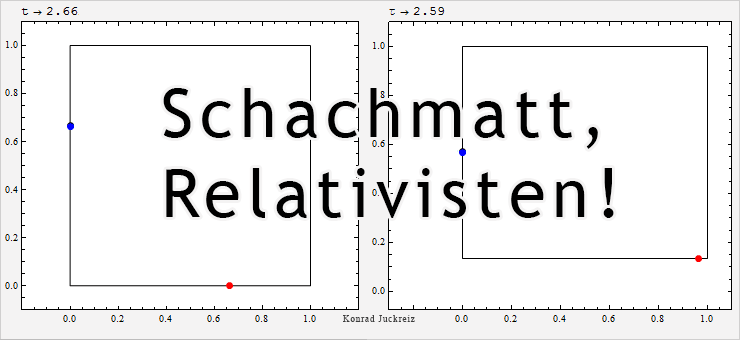
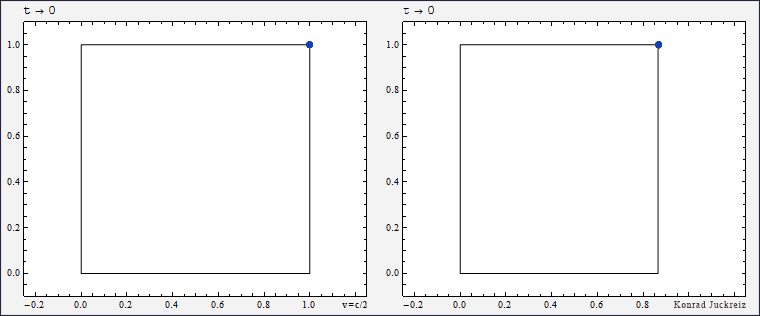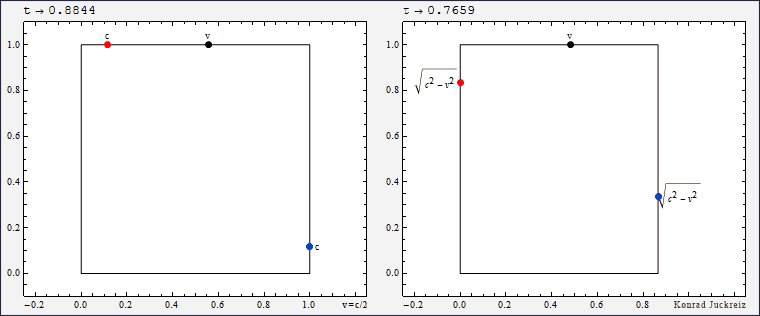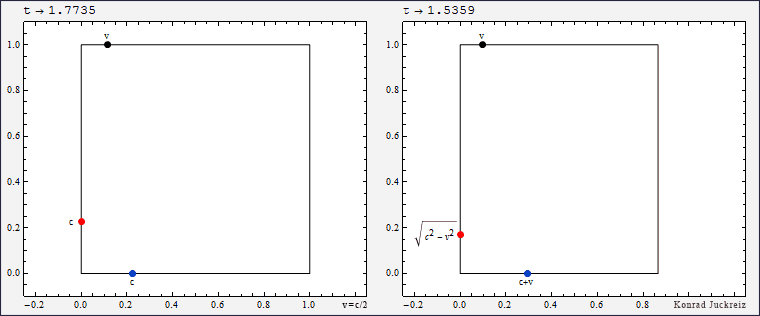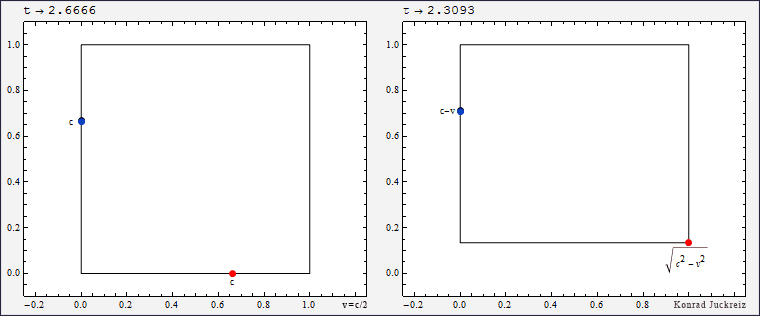
Wie Sie sehen würde bei τ=√3 Sekunden sowohl das blau als auch das rot dargestellte Signal mit Überlichtgeschwindigkeit, im Limit sogar instantan, von einer Position auf die nächste springen. Da die Lichtgeschwindigkeit aber die Geschwindigkeit des Lichts ist, kann sich Licht nicht mit Überlichtgeschwindigkeit bewegen (und noch weniger an einem Ort verschwinden und am anderen wieder auftauchen).